Calculating trigonometric functions on a simple microprocessor, the CORDIC method

Ian Todd

Simple microprocessors, like the PIC series, are unable to directly calculate trigonometric functions when programmed in assembly language. In many cases users overcome this by using Look-Up Tables (LUTs), but this approach lacks the finest resolution, unless large amounts of memory are used to store huge tables.

I originally used LUTs, but while reading the literature, I came across an ingenious technique which enables an accurate calculation of some of the trig functions on simple processors.

It is called the CORDIC method, an acronym from COrdinate Rotation DIgital Computer, which is credited to Jack Volder (ref 1). He was working on an aircraft navigation computer which required trigonometric calculations. This was for the Convair B-58 Hustler bomber to replace the analogue resolver in use at that time. This was in 1959, in the very early days of digital techniques.

Somewhat surprisingly, the technique is apparently still not well known despite many pocket calculators using the method for trig functions.

In this article I’ll first attempt to explain in a simple way how to just use the CORDIC method to perform some trigonometric functions. After that I’ll give an explanation of why the calculations work as they do.

The CORDIC method requires a short precalculated LUT of just 16 entries.

For example:

I found that numbers on my microprocessor could be adequately stored as binary Q8.16 format. This is a signed fixed point representation occupying 24 bits. The first 8 bits are the signed integer part of the number followed, after a “virtual” radix point (binary point), by 16 bits for the fractional part. This is fine for numbers ranging from -128 to +127, which is ample for ±90 degrees. Obviously more bits could be used if they were necessary.

Calculating sine and cosine

The simplest form of the CORDIC method is to calculate the sine and cosine of an angle.

We set the following:
x = 0.60725 (The CORDIC scaling factor explained at the end)
y =0
Acc = angle for which we require the sine or cosine

x_iter+1 = x_iter - y_iter * d * 2^-iter

y_iter+1 = y_iter + x_iter * d * 2^-iter

Acc_iter+1 = Acc_iter - d * arctan( 2^-iter)

The method to calculate the next value of x (x_iter+1) becomes:

1. Take the previous value of y and shift it iter places right. This is the same as multiplying by 2^-iter
2. Use d (which is plus or minus one) to determine the sign of the result.
3. Subtract this from the previous x value.

The next value of Acc is obtained by:
1. Getting the appropriate arctan(2^-iter) from the LUT
2. Multiply this by d (which is either plus or minus one)
3. Subtract this from the previous Acc value

Calculating an arctangent

Calculating an arctangent uses the same equations, as above but d is determined by testing the value of y_iter. If it’s greater than 0 then d is -1, otherwise d = +1.
The values of x and y are initialised to either the x and y components of the tangent, or to one and the tangent value respectively.
Acc is set to 0
After the required number of iterations the required arctan is held in Acc This works well for up to 90 degrees where both x and y have positive values. However inspecting the signs of the initial values of x and y permits determination of the quadrant in question and the appropriate correction can be applied. The CORDIC calculator should be loaded with the absolute values of x and y (i.e. make both numbers positive) and the following changes made to the arctan calculated.

Calculating an arcsine

Calculating an arcsine is a similar process but note the version shown in the Andraka paper (ref. 2) contains a typographical error

Acc_iter+1 = Acc_iter - d * arctan(2^-iter)
should read
Acc_iter+1 = Acc_iter + d * arctan(2^-iter)

However at large angles near 90 degrees and at certain smaller angles it fails to converge correctly, and can give quite large inaccuracies.
Using a technique called “double iteration” avoids this problem.

The starting conditions are:
x=1
y= 0
Acc = 0
sine = The sine of which we require the arcsine

Again we perform an iterative calculation:

Calculating an arccosine

Replace equ.1 with
If x_iter+1 is greater than cosine then d = 1 otherwise d = -1

Replace equ.2 with
If y_iter+1 < 0 then d = 1 this prevents errors at small angles.

Replace equ.3 with
cosine = cosine + (cosine * (2^-iter) * (2^-iter))

In many cases the arccosine can be more rapidly calculated by subtracting the arcsine from 90 if the arcsine is already available.

How the CORDIC technique works

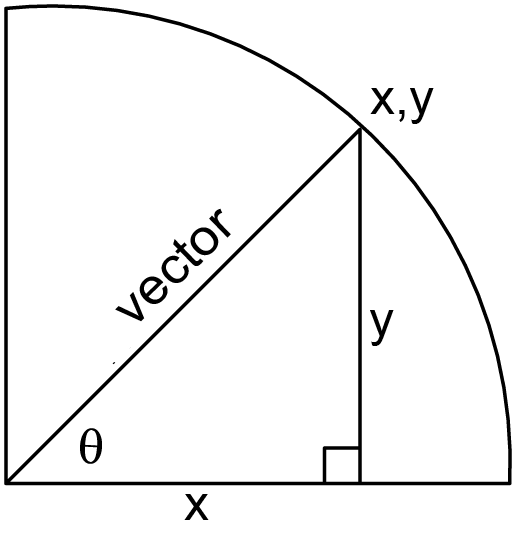Start with a vector of unit length which is drawn at an angle θ to the x axis as shown in the diagram. The coordinates of this vector are 0,0 and x,y . A line drawn vertically from the end of the vector intersects the x axis at the value of the x coordinate and has a length y which is the y coordinate value. This makes a right angle triangle. From simple trigonometry the sine of angle θ is the opposite (y) over the hypotenuse. Because the vector (hypotenuse) has a length of one (unit length), the sine is just the value y. Similarly the cosine of angle θ, adjacent over hypotenuse, is the value of x.

So if we start with a unit vector on the x axis and rotate it about the origin by an angle, the values of x and y are the cosine and sine of that angle.

The traditional method to calculate the sine and cosine of an angle θ starts with a vector along the x axis. The vector is then rotated some degrees anticlockwise (positive direction) and the angle rotated is compared to the angle θ. If the rotated angle is less, then a further rotation is done by a smaller positive angle. The two rotation angles are added together. If the initial rotation was greater than angle θ then the following rotation is in a negative direction and the angle is subtracted from the initial one. This process is repeated using ever smaller rotations each either adding to, or subtracting from, the previous total angle, causing the total to converge to the starting angle θ.

The new x and y coordinates after a rotation through θ degrees would normally be calculated using the Givens equations,

x_new = x * cos(θ) - y * sin(θ)
y_new = y * cos(θ) + x * sin(θ)

Volder’s clever idea was to convert the sin(θ) to cos(θ) * tan(θ),

x_new = x * cos(θ) - y * cos(θ) * tan(θ)
y_new = y * cos(θ) + x * cos(θ) * tan(θ)

x_new = cos(θ) * (x - y * tan(θ))
y_new =cos(θ) * (y + x * tan(θ))

x_new = (x - y * tan(θ))
y_new = (y + x * tan(θ))

He also restricted the rotation angles (θ), to arctan(2⁰) through to arctan(2^-15), in that way multiplying by tan(θ) becomes a simple binary shift.

A further equation was added to sum the angles through which the vector was rotated

Acc_iter+1 = Acc_iter - d * arctan( 2 ^-iter)

However the extracted cos(θ) term leads to the CORDIC routine returning scaled values in the case of sine/cosine calculations.

For each iteration iter, the scaling factor, K_iter = cos(arctan(2^-iter))

Volder’s modifications made the calculations quite straightforward on a simple microprocessor requiring only addition, subtraction, and division by powers of two, which is easy in a binary system, as it just involves shifting the number the required number of bits to the right.

This CORDIC implementation only works for angles between +90 and -90 degrees, but there are methods to extend the range. For these, and a more rigorous mathematical description of all of the above, see Ray Andraka’s paper (ref. 2); a good reference.

Other elementary functions are also calculable by this method, for instance in 1971, J.S. Walther, (ref. 3) at Hewlett-Packard, extended the CORDIC method to do multiplication, division, sin, cos, tan, arctan, sinh, cosh, tanh, arctanh, ln, exp and square root.. Such things, however, are beyond the scope of this webpage .

References

Copies of these references are readily available on the internet.

1. Jack E. Volder, The CORDIC Trigonometric Computing Technique, IRE Transactions on Electronic Computers, Vol. EC-8, pp 330-334, 1959

2. Ray Andraka, A survey of CORDIC algorithms for FPGA based computers, Proceedings of the 1998 ACM/SIGDA sixth international symposium on field programmable gate arrays. Feb 22-24, 1998. Monterey CA. pp191-200

3. Walther, J.S., “A unified algorithm for elementary functions,” Spring Joint Computer Conf., 1971, proc., pp 379-385.